Czas na kolejny post z tych bardziej naukowych, dotyczący projektu easyGALib. Jego tematem będzie selekcja w algorytmach genetycznych, czyli sposoby na wybieranie chromosomów, na podstawie których tworzone jest każde kolejne pokolenie, które ma być lepiej dopasowane niż poprzednie.
W poście o sercu biblioteki widziałeś już algorytm, który zastosowałem w kodzie, więc przyszła pora na pracę nad jego poszczególnymi fragmentami. Celowo ominę dwa z nich – inicjalizację populacji, bo to po prostu takie wstępne uruchomienie algorytmu i obliczenie funkcji dopasowania, bo jak pewnie pamiętasz, tę metodę ma nam dostarczyć użytkownik korzystający z easyGALib. Kolejnym bloczkiem jest selekcja chromosomów.
Selekcja w algorytmach genetycznych
Pytanie, które pewnie przychodzi Ci teraz do głowy, to po co mamy w ogóle robić jakąś selekcję? Czy chodzi o to, żeby tych w obuwiu sportowym nie wpuszczać? Tak dokładnie! W pewnym sensie… Teoria Darwina mówi, że najlepiej dostosowane osobniki powinny przeżyć i wydać na świat potomstwo. W algorytmach genetycznych wybiera się więc najlepsze chromosomy ze starszej populacji i krzyżuje między sobą, dzięki czemu uzyskujemy nowe, stanowiące kolejne pokolenie. Problemem samym w sobie jest natomiast to, jak wybrać te konkretne osobniki, które będą stanowić podstawę kolejnej generacji. Istnieje kilka różnych rozwiązań i każde z nich ma swoje wady i zalety. Sam kod biblioteki postaram się przygotować w taki sposób, aby łatwo można było podmienić metodę selekcji, czy nawet wybrać ją za pomocą odpowiedniego parametru. W tym poście skupię się jednak na kilku rodzajach selekcji, z których możemy skorzystać.
Ruletka
Na początek coś dla hazardzistów, czyli metoda ruletki. Chromosomy dobierane są w odniesieniu do ich obliczonego wcześniej dopasowania do rozwiązywanego problemu – im lepszy osobnik, tym większa szansa, że zostanie wybrany. Możesz to sobie zobrazować w ten sposób, że cała populacja to koło ruletki, a im lepiej jest dopasowany dany chromosom, tym więcej miejsca na tym kole zajmuje. Później zaczynamy kręcić i czekamy co nam wypadnie.
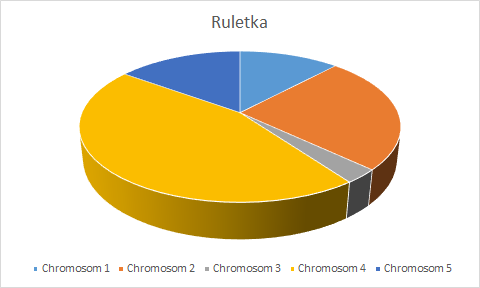
Na wykresie wyraźnie widać, że największą szansę na wylosowanie będzie miał chromosom 4, jednak jak to w ruletce, nie jesteśmy do końca pewni co najlepiej obstawić. Wada tej metody ujawnia się w momencie, gdy mamy osobnika zajmującego na przykład 90% powierzchni koła – inne w zasadzie nie mają wielkiej szansy na wylosowanie, przez co możemy nie dotrzeć do lepszego wyniku.
Ranking
Problem opisany powyżej stara się zwalczać metoda rankingowa. Tutaj znowu mamy do czynienia z kołem na którym będziemy losować, jednak chromosomy rozkładane są w nieco inny sposób. Najpierw układany jest ranking chromosomów od najgorszego, który zajmuje 1 miejsce, do najlepszego, który zajmuje miejsce N, gdzie N to liczba chromosomów w populacji. Następnie traktujemy to jako ilość udziałów danego osobnika w całej funkcji dopasowania i proporcjonalnie przydzielamy miejsce na planie koła.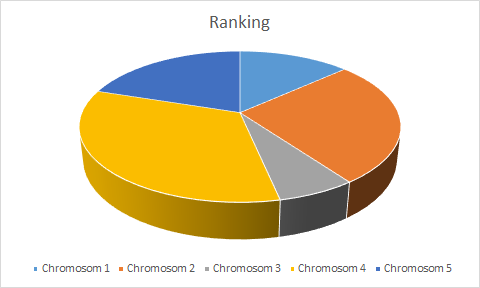
W tym przypadku widać, że przeważający wcześniej chromosom 4 ustąpił nieco miejsca innym. Nadal wszystko jest proporcjonalne względem tego jak dopasowany jest dany osobnik, jednak eliminujemy możliwość dużej przewagi jednego z nich nad resztą. Skutkiem takiego działania jest jednak to, że na końcu chromosomy będą niewiele się od siebie różnić.
Stabilny stan (eng. Steady-state selection)
Nie jest to do końca metoda selekcji, a raczej idea operowania kolejnymi populacjami. Pomysł jest taki, by większa część chromosomów „przetrwała” do kolejnej generacji, a zmiany dotyczą jedynie grupki najsłabszych osobników. Działamy więc następująco:
- Wybieramy kilka najlepszych chromosomów
- Krzyżujemy je ze sobą
- Grupkę najsłabszych zamieniamy nowo utworzonymi
- Cała reszta pozostaje bez zmian
Elitaryzm
Korzystając z dwóch pierwszych metod może nastąpić sytuacja, że będziemy mieć już super wypasiony chromosom, dopasowany najlepiej jak się da, a w którejś generacji skrzyżujemy go z innym i odpadnie z dalszej gry. Nie chcemy takich sytuacji, więc warto wprowadzić elitaryzm, czyli z każdej generacji wybieramy jakąś elitę wśród chromosomów, taką wręcz szlachtę i kopiujemy ją do nowej populacji. W ten sposób mamy pewność, że na końcu zawsze będziemy mieć tego jednego, najlepiej dopasowanego osobnika. Taki zabieg znacznie poprawia działanie i efektywność algorytmu genetycznego!
Jak widać w algorytmach genetycznych cały czas przenikamy się ze światem przyrody i nawet teoria Darwina znajdzie tu swoje zastosowanie. Sama selekcja w algorytmach genetycznych pomaga nam natomiast operować na jak najlepszych osobnikach, aby z czasem osiągać co raz lepsze wyniki. Wkrótce na blogu pojawi się oczywiście implementacja powyższych metod w easyGALib, so stay tuned!
Dodaj komentarz