Jak już dowiedziałeś się w ostatnim poście, dotarliśmy do momentu pierwszego uruchomienia easyGALib. Po poprawieniu drobnych błędów dostaliśmy wynik, tyle że nadal problemem jest to, że nie zawiera poprawnego rozwiązania. Pytanie więc, dlaczego same zera?
Chwilę minęło od ostatniego posta i uwierz, dużo wcześniej chciałem rozjaśnić nad czym jeszcze powinniśmy popracować. W międzyczasie postanowiłem jednak przenieść bloga z Azure’a na inny hosting ze względu na pewne problemy z wydajnością bazy, stąd przez kilkanaście godzin był nieobecny w Internecie. Pierwsze podejście zakończyło się jednak niepowodzeniem i powtórnie DNSy ustawiłem na adres chmury Microsoftu. Okazuje się, że nie będzie to taki szybki proces, więc odłożę go jeszcze w czasie, aż do zakończenia konkursu „Daj się poznać”.
Dlaczego same zera
Wracając do tematu, postanowiłem przejść od początku do końca po działaniu algorytmu i wskazać kilka błędów, przez które nie udało się nam uzyskać poprawnego wyniku. A więc po kolei, gdzie mamy winowajców?
- Początkowa wartość genów
Zaglądając pierwszy raz w populację genów, nie sposób było oprzeć się wrażeniu, że jakoś zaraz po inicjalizacji za dużo jest zer i jedynek. Miały być przecież liczby od 0 do 1000. Oczywiście niepotrzebnie wartość początkową losowaliśmy, a następnie dzieliliśmy przez jeszcze inną. Takie coś miałoby sens dla liczb zmiennoprzecinkowych, a tutaj jest bezużyteczne i właśnie przez to tak dużo zer i jedynek. Końcowo losowanie wartości w metodzie ChildrenInit powinno mieć postać:
int val = _rdm.Next(0, 1000);
- Random
Przeglądając działanie algorytmu po raz drugi, zauważyłem że jakoś powstało dużo identycznych chromosomów. Jak to możliwe? Doświadczenie podpowiada od razu jedną rzecz – generator liczb losowych. Tak się składa, że klasa Random i generowane przez nią liczby pseudolosowe, są zależne od czasu w którym została zainicjowana. Skoro więc w pętli używaliśmy jej za każdym razem od nowa, w prawie że jednakowym czasie, to i uzyskane sekwencje liczb były jednakowe. Rozwiązanie jest więc bardzo proste, obiekt konstruujemy raz, a później tylko przekazujemy go przez referencję.
- Zwracana wartość funkcji dopasowania
var distance = 0;
for (int i = 1; i < 4; i++)
{
distance += cities[genes[i], genes[i - 1]];
}
if (distance == 0)
{
return 0;
}
return 1 / distance;
Widzisz w powyższym kodzie jakiś błąd? Nie? To super, bo błędu tu nie ma. Metoda jednak zwróci liczbę całkowitą. Dlaczego? Bo dzielimy liczbę całkowitą przez całkowitą. W końcu to Ty jesteś panem, a kompilator sługą i robi to co mu każesz! W tym przypadku chcesz dzielenia liczb całkowitych, to i wynik będzie całkowity. Jak chcesz wynik zmiennoprzecinkowy to sobie zrzutuj dzielone wartości na double i wtedy trafisz na odpowiednie przeładowanie operatora „/” 🙂
Jaki był wynik powyższych poprawek? Taki:

Czyli jest już OK, jeżeli chodzi o losowanie początkowej wartości. Dla bezpieczeństwa przeszedłem jeszcze po wszystkich krokach i wygląda na to że wszystko działa prawidłowo. Dlaczego więc nie mamy nadal poprawnego wyniku?
Nikła szansa na sukces
Wróćmy jeszcze raz do problemu wędrownego sprzedawcy. Jego rozwiązaniem ma być na przykład taki zestaw [0,2,1,3], czyli cztery miasta, ułożone w odpowiedniej kolejności. Teraz pytanie, jaką mamy szansę losując za każdym razem od 0 do 1000 uzyskać taki właśnie zestaw, gdzie są jedynie niepowtarzające się cyfry od 0 do 3? Szanse mniejsze niż w totku niestety. Dodatkowo nie pomagamy naszemu algorytmowi, bo w funkcji dopasowania nie mówimy w żaden sposób, że jeżeli liczby się nie powtarzają albo są w przedziale 0-3, to już jest coś lepiej. Po prostu od razu zwracamy wartość dopasowania 0. Tym sposobem algorytm genetyczny szuka, ale w zasadzie nie ma pojęcia w jakim kierunku powinien iść.
Jak zatem rozwiązać tę sytuację? Na obecną chwilę możemy zrobić jedną rzecz. Wrócić do generowania wartości początkowej genu i ustawić ją w zakresie 0 do 10! Tym sposobem wielokrotnie zwiększymy szansę, że w populacji pojawi się chromosom spełniający żądane warunki. Uruchamiamy więc algorytm i wynik jest następujący:
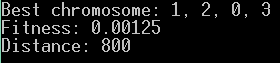
Jeszcze raz i tym razem:
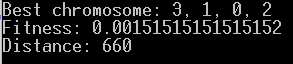
Prawie za każdym razem uzyskujemy lepszy, lub gorszy wynik. Nie chcemy jednak, by była potrzeba modyfikacji biblioteki ze względu na problem, który w danym momencie rozwiązujemy. Będziemy tu mieć więc dwa wyjścia. Po pierwsze możemy wprowadzić kolejny parametr, który będzie regulował zakres wartości, na których operujemy. Po drugie możemy zająć się tematem ulepszenia inicjalizacji populacji, aby była większa szansa na to, że pojawi się chromosom, który będzie rozwiązaniem. Możemy przecież inicjalizację przeprowadzić kilka razy i z każdej z nich wybierać najlepsze osobniki. Tym właśnie zajmiemy się w kolejnym poście!


Dodaj komentarz